When I select puzzles to accompany this column, I stick to the plain vanilla. The stipulation must be short and sweet, and one move solutions must be accepted (though I like to include a few further words of explanation). Alas, a thousand such puzzles can never do justice to the wondrous ingenuity of chess composers.
Longer mating problems and ‘studies’ (where the objective is to find a winning or drawing sequence) allow considerably more artistic scope. Then there are genres which maintain the rules of movement but subvert the players’ objectives. Those include helpmates (in which both sides choreograph their moves to engineer a checkmate) and selfmates (in which one side attempts to force the other to deliver checkmate). Selfmates I find particularly mind-bending, though the aesthetic dividends can be considerable.
All these were featured at the World Team Chess Solving Championship, held in Riga in late July. Solving competitions are like a series of exams, in which competitors solve problems against the clock. The Polish team were a strong favourite, having won all but one of the team events since 2009. Two of their competitors, Piotr Murdzia and Kacper Piorun, have 14 individual world solving championships between them.
But the British team of John Nunn, David Hodge and Jonathan Mestel are all proficient solvers (Nunn and Mestel are former individual world solving champions, and Hodge is the reigning British solving champion). The race was especially tight this year, with both Britain and Poland finishing on the same number of points, but Britain took the title thanks to a better tiebreak: they had taken a bit less time.
One side event in Riga featured an even more niche theme – Retro solving. ‘Retro’ refers to the need to deduce something about the preceding moves, based on a diagram position. One classic example, below, is a mate in 2 with a twist, composed by Thomas Dawson in 1914. At first sight, both en passant captures 1 gxf6 and 1 cxd6 do the trick. But exactly 10 black units are missing, and white’s eccentric pawn structure entails at least 10 captures since the start of the game. If black’s preceding move were d7-d5, the Bc8 could never have been captured by a pawn, so the last move must have been f7-f5. Ergo 1 gxf6 is the unique solution.
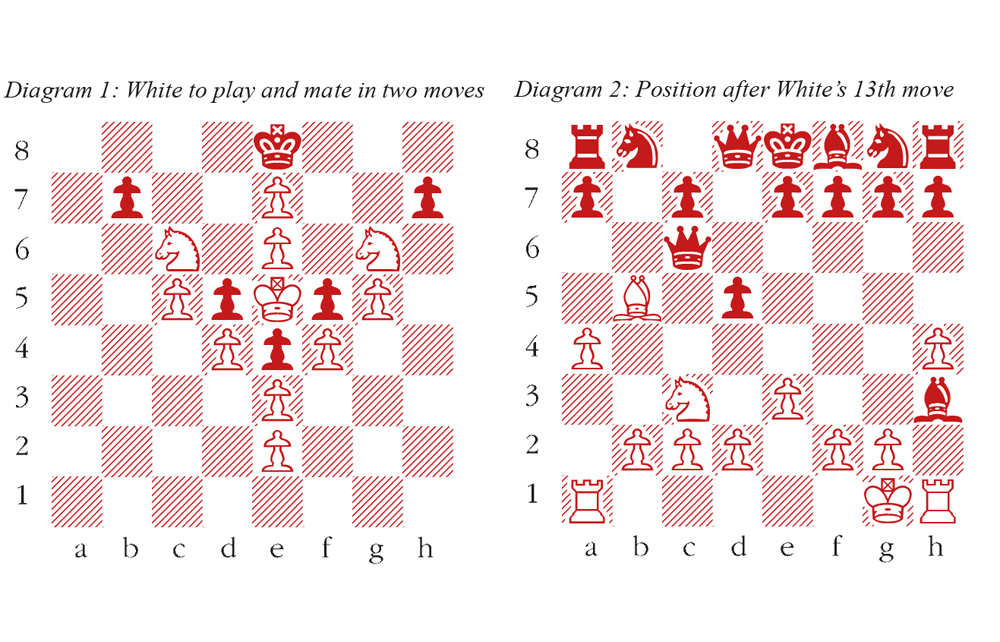
The second diagram shows a ‘proof game’, presented as a problem in Riga, and composed by Markus Ott in 1983. The diagram shows the position after white’s 13th move, and the task is simply to deduce all the moves from the start position up to the diagram. This is well worth attempting, but harder than it looks, although evidently, the pawn from b7 must have promoted to a queen. The solution reveals a very neat surprise.
Solution:
1 a4 b6 2 Ra3 b5 3 Rg3 b4 4 Na3 bxa3 5 e3 a2 6 Bb5 a1=Q 7 Ne2 Qxc1 8 O-O Qxd1 9 Nc3 Qf3 10 h4 Qc6 11 Rh3 d5 12 Rh1 Bh3 13 Ra1





Comments